[알고리즘] 삽입정렬(Insertion Sort) - Python

1. 삽입정렬의 원리

(1) 삽입정렬은 2번째 index에서 시작합니다 (코드 작성시 주의)

(2) 현재의 key가 앞의 숫자보다 큰지 작은지 확인하고,

• 앞의 숫자 < key 이면: 순서 그대로 유지
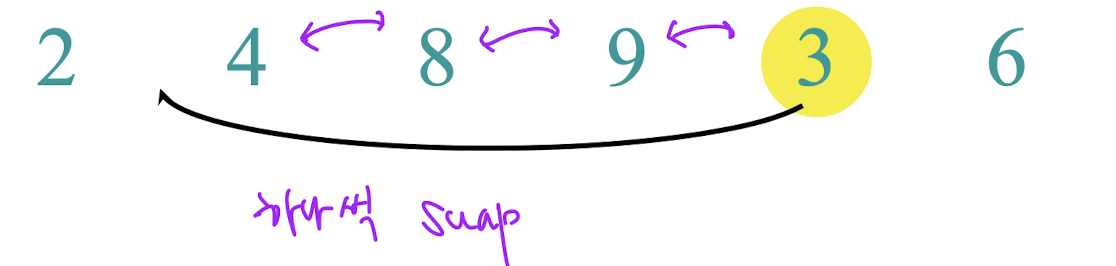
• 앞의 숫자 > key 이면: 서로 위치 바꾸기 (Swap)

(3) 이후, key를 오른쪽으로 한 칸 옮기기

(4) key인 4가 8보다 작으므로 swap

(5) 작업이 끝났으니 다시 key 한 자리 옮기기

(6) 위 과정을 계속 반복하여 최종 정렬된 array 생성

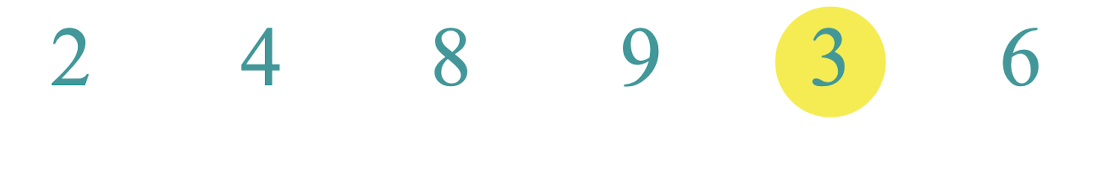
2. 삽입정렬 Python 코드

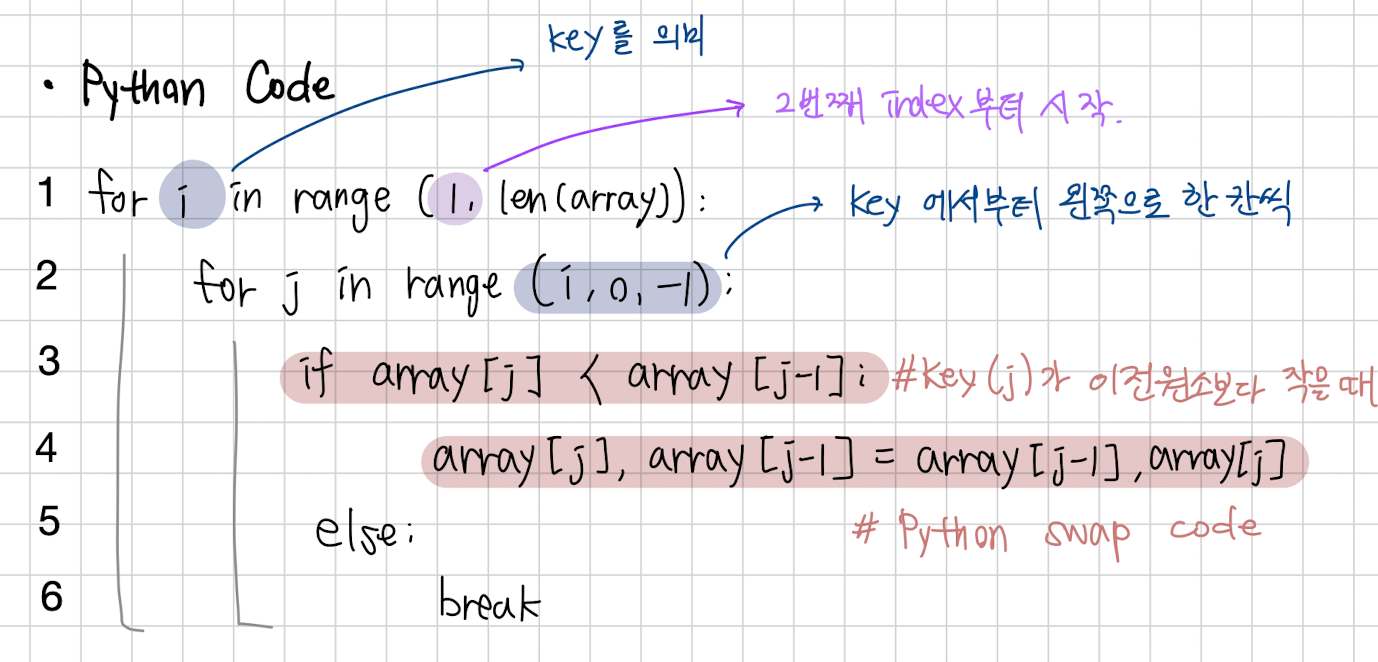
1. index “i”는 위 설명에서의 Key를 의미합니다. 또한, range를 1에서부터 시작하여 2번째 index부터 key로 설정될 수 있게 합니다.

2. key에서부터 왼쪽으로 대소비교를 하여 정렬을 할 수 있도록 inner loop를 설정해줍니다.

3. Key가 이전 원소보다 작으면,

4. Python의 swap코드 (a,b = b,a)를 이용하여 swap 진행

아래는 삽입정렬에 대한 Python 전체 코드와,

Array가 오름차순 ascending[1, 2, 3, … , 9999, 10000]일 때의 삽입 정렬 Array가 랜덤으로 섞여있을 때의 삽입 정렬 Array가 내림차순 descending[10000, 9999, 9998, … , 2, 1] 일 때의 삽입 정렬 의 수행시간을 비교하는 코드입니다.

# 1. Implement Insertion Sort  
import time
import random

def insertion_sort(list):
    for i in range(1, len(list)):
        for j in range(i, 0, -1):
            if list[j] < list[j-1]:
                list[j], list[j-1] = list[j-1], list[j]
            else:
                break

def insertion_sort_time(list):
    start_time = time.time()
    insertion_sort(list)
    end_time = time.time()
    return end_time - start_time


# a. Perform sorting in ascending order  on [1,2,3,4,5,6,........9999,10000] 
#    and compute the time for the execution.
list_a = list(range(1, 10001))
time_a = insertion_sort_time(list_a)
print("ascending order sorting time (sec):", time_a)

# b. Random shuffle the number [1,2,3,4,5,6,....9999,10000]  
#    and sort the array in ascending order, compute the time for the execution
list_b = list(range(1, 10001))
random.shuffle(list_b)
time_b = insertion_sort_time(list_b)
print("shuffled array sorting time (sec):", time_b)

# c. Perform sorting in descending order on [10000,9999,9998, ..... 3,2,1] 
#     and compute the time for the execution.  
list_c = list(range(10000, 0, -1))
time_c = insertion_sort_time(list_c)
print("descending order sorting time (sec):", time_c)



# Result
# ascending order sorting time (sec): 0.0020825862884521484
# shuffled array sorting time (sec): 2.6333789825439453
# descending order sorting time (sec): 5.20855188369751

Ascending인 경우 굉장히 빠른 속도로 정렬한 것을 볼 수 있고,

정렬된 방식에 따라 위와 같은 정렬 시간의 차이를 보이는 것을 알 수 있습니다.

3. 삽입정렬 시간복잡도/공간복잡도

시간복잡도:

• 위 정렬 시간 비교에서 나타났듯이, Best Case는 오름차순으로 정렬되어 있는 경우입니다.
• 오름차순의 경우 1 ~ n의 바깥의 for loop 하나만 통과하면 되므로 O(n)의 시간복잡도를 가지는 것을 알 수 있습니다.
• Worst Case는 내림차순으로 정렬되어 있는 경우입니다.
• 내림차순의 경우 1 ~ n의 Outer loop와 1 ~ n의 Inner loop를 모두 통과해야 하므로 n × n = n^2, 즉 O(n^2)입니다.
• 따라서, Insertion Sort의 Time Complexity는 O(n^2)입니다.

공간복잡도:

• Insertion Sort는 정렬 수행 과정에서 추가적인 보조 공간(Auxiliary Space)를 필요로 하지 않습니다.
• 물론 Swap하는 과정에서 공간 한 자리가 필요하긴 하지만, 너무 작기 때문에 무시합니다.
• 따라서, Insertion Sort는 Auxiliary Space를 필요로하지 않는 In-place Sort입니다.