[알고리즘] 퀵 정렬 (Quick Sort) - Python

1. 퀵 정렬의 원리

퀵 정렬은 Divide and Conquer 방식을 따릅니다.

• Divide 단계에서는 Partition 방식을 통해 “pivot”을 기준으로 두개의 array로 나눕니다. 그 다음, pivot보다 작은 원소는 pivot 기준 왼쪽에 위치하도록, pivot보다 큰 원소는 오른쪽에 위치하도록 합니다.
• Conquer 단계에서는 재귀적으로 두개의 subarrays를 정렬합니다.

퀵 정렬의 Partition 단계에는 대표적으로 Hoare 방식과 Lomuto 방식이 있습니다.

• Hoare 방식: 양 끝에서 가운데로의 진행방향
• Lomuto 방식: 한쪽 끝에서 다른쪽 끝으로의 진행방향

본 내용은 로무토(Lomuto) 방식의 퀵 정렬에 대한 설명입니다.

---

아래는 간략한 Lomuto Partition 과정 설명입니다.

pivot을 설정하는 방법은 다양합니다. 맨 처음 원소를 pivot으로 선택하는 방법, 랜덤으로 선택하는 방법, 가운데로 선택하는 방법, 맨 마지막 원소를 선택하는 방법 등이 있습니다. 해당 예시에서는 맨 처음 원소를 pivot으로 선택하는 방법을 채택합니다.

• 맨 처음의 원소를 pivot으로 설정한 후, pivot과 맨 마지막 원소를 swap합니다.
• pivot과 보라색 화살표(j)가 가리키는 원소(A[j])를 비교하여, A[j] < pivot 이면, A[i] 와 A[j]를 swap 합니다. A[j] >= pivot이면 swap은 이루어지지 않습니다.
• 보라색 화살표(j)는 비교 작업이 한 번 끝나면 매 시행마다 한 칸 무조건 증가합니다.
• 초록색 화살표(i)는 swap이 일어났을 때만 한 칸 증가하고, 보라색 화살표가 array 전체를 순회 완료했을 때, 마지막으로 pivot과 위치를 swap합니다.

아래의 예시를 통해 자세히 보겠습니다.

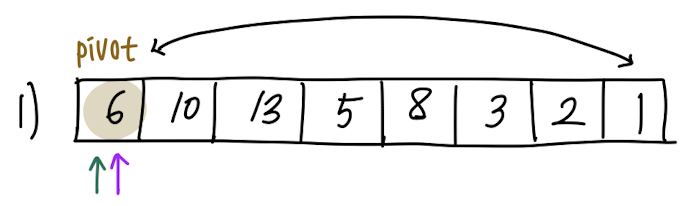
맨 앞 원소를 pivot으로 설정했습니다.

pivot을 설정하고, 맨 마지막 원소와 swap합니다.

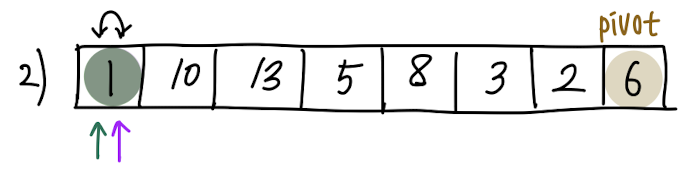
처음엔 i(초록색 화살표), j(보라색 화살표) 인덱스가 맨 처음 원소로 초기화되어 있습니다.

초기화 상태는 다 보았으니 이제 비교를 시작합니다.

보라색 화살표(j)의 원소(A[j])와 pivot값을 비교합니다. 1 < 6 즉, A[j] < pivot 이므로, A[i]와 A[j]를 swap합니다. (현재의 경우에서는 swap 해도 그대로입니다.)

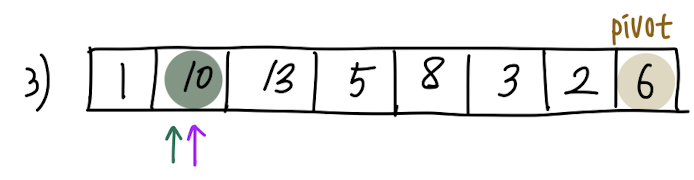
한 번의 비교 작업이 끝났기 때문에, 보라색 화살표(j)는 한 칸 증가합니다.

swap이 이루어졌기 때문에, 초록색 화살표(i) 또한 한 칸 증가합니다.

이제 다시 보라색 원소와 pivot을 비교합니다. 10 > 6 즉, A[j] > pivot 이므로 swap은 이루어지지 않습니다.

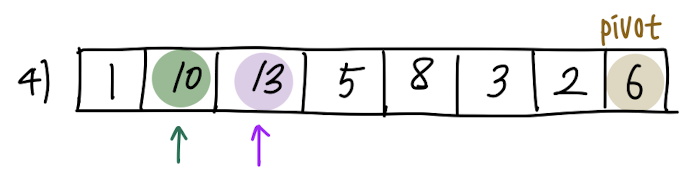
swap이 이루어지지 않았으므로, 보라색 화살표(j)만 한 칸 증가하고, 초록색 화살표(i)는 그대로 남아있습니다.

다시 보라색 원소(A[j])와 pivot을 비교하면, A[j] > pivot 입니다.

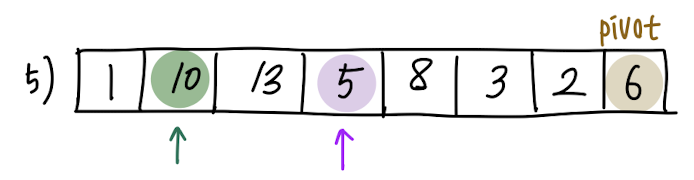
swap이 이루어지지 않았으므로, 보라색 화살표(j)만 한 칸 증가하고, 초록색 화살표(i)는 그대로 남아있습니다.

다시 보라색 원소(A[j])와 pivot을 비교하면, 이번에는 5 < 6 즉, A[j] < pivot 입니다.

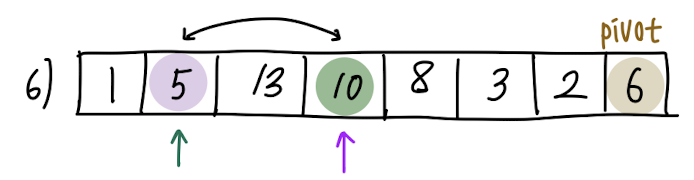
A[j] < pivot이므로, 초록색 원소(A[i])와 보라색 원소(A[j])를 swap 합니다.

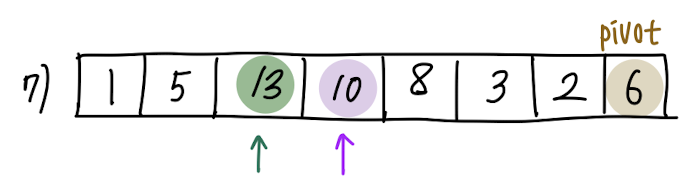
Swap이 이루어 졌으므로, 초록색 화살표(i)도 한 칸 증가하고, 보라색 화살표(j)도 한 칸 증가합니다.

다시 보라색 원소(A[j])와 pivot의 대소비교를 진행합니다. 10 > 6, A[j] > pivot입니다.

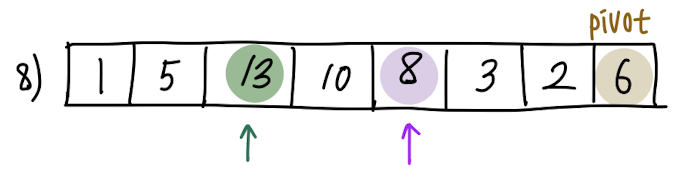
A[j] > pivot 이므로, 보라색 화살표(j)만 한 칸 증가합니다.

위와 같은 과정을 계속 반복하면 아래와 같습니다.

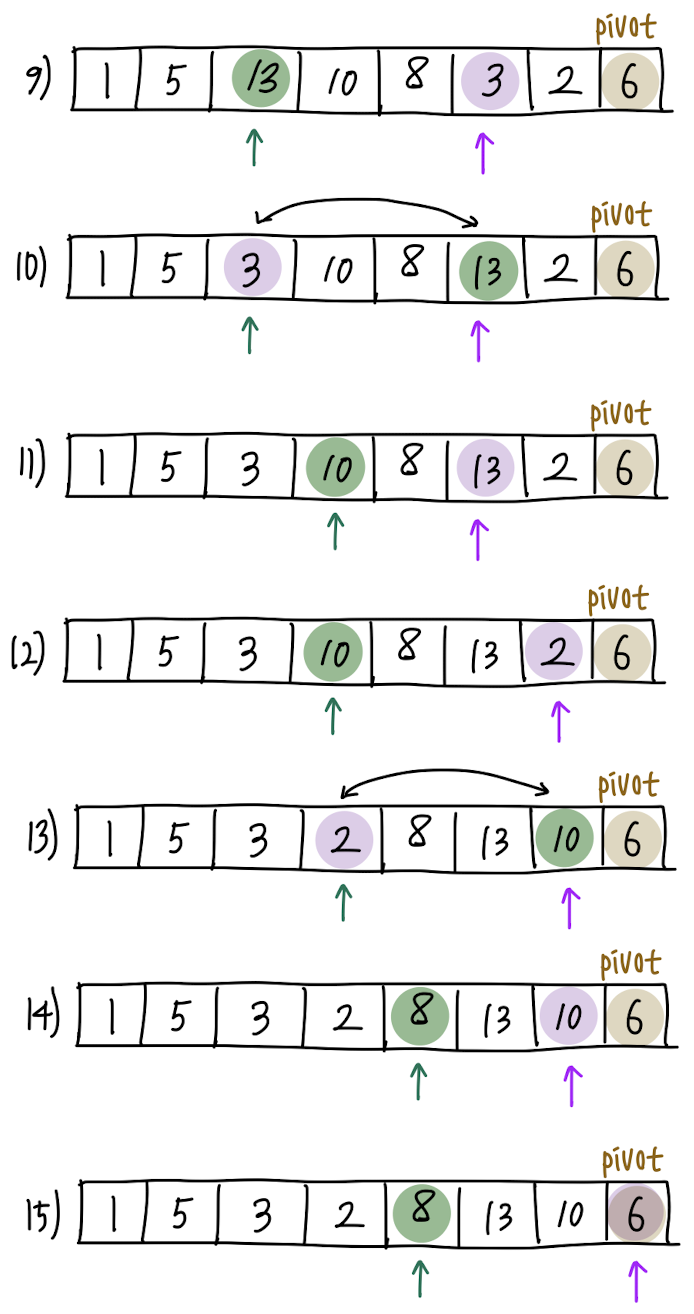
15번에서 보라색 화살표(j)가 pivot의 위치에 도달한 것을 볼 수 있습니다. j가 array를 모두 순회했다는 뜻입니다.

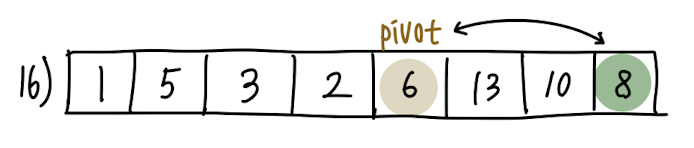
j가 array를 모두 순회했으면, 마지막으로 pivot과 A[i]를 swap 하는 것으로 이 Partition 과정이 마무리 됩니다.

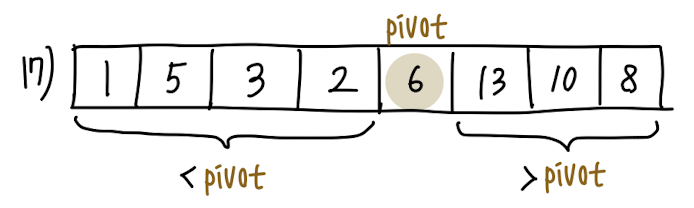
해당 partition 과정을 거치면, pivot을 기준으로

pivot 왼쪽에는 pivot의 원소보다 더 작은 원소들로,

pivot의 오른쪽에는 pivot 원소보다 더 큰 원소들로 분할(partition)됩니다.

Partition 작업을 마쳤으면, pivot을 기준으로 왼쪽/오른쪽으로 나누어진 array에 각각 재귀적으로 partition을 반복 수행합니다.

2. 퀵 정렬 Python 코드

def partition(A, low, high):
    pivot_idx = low #pivot을 처음 원소로 설정
    pivot = A[pivot_idx]

    A[pivot_idx], A[high] = A[high], A[pivot_idx] #맨 처음 pivot과 마지막 원소를 swap

    i = low #low 자리에서 i 시작
    for j in range(low, high): #j가 array 처음부터 끝까지 도는 동안
        if A[j] < pivot: #A[j]가 pivot보다 작으면
            A[i], A[j] = A[j], A[i] #A[i]와 A[j] swap
            i += 1 #swap 이루어졌으면 i에 +1

    pivot_idx = i
    A[pivot_idx], A[high] = A[high], A[pivot_idx] #loop 마치면 A[i]와 pivot swap

    return pivot_idx

위 코드는 partition에 대한 코드입니다.

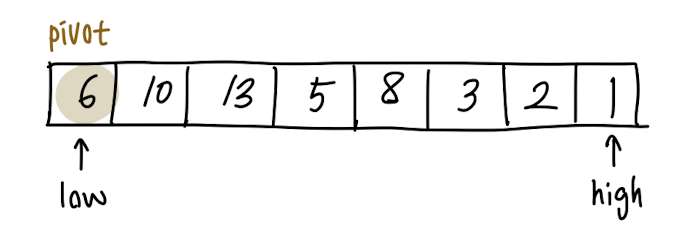
위와 같은 array 상황에서 partition을 수행합니다.

---

다음은 partition을 재귀적으로 수행하는 quick_sort 함수 코드입니다.

def quick_sort(A, low, high):
    if low < high:
        pivot_idx = partition(A, low, high) #pivot 기준 partition 진행
        quick_sort(A, low, pivot_idx - 1) #partition의 왼쪽 array에 대해 재귀
        quick_sort(A, pivot_idx + 1, high) #partition의 오른쪽 array에 대해 재귀

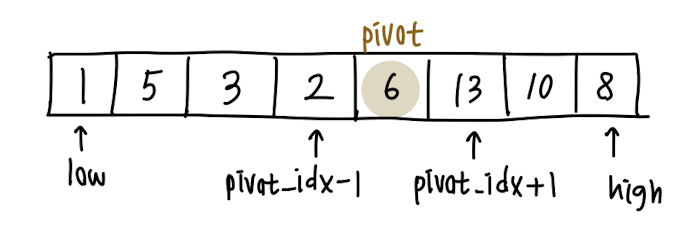
피봇의 인덱스(pivot_idx)를 사용하여, 왼쪽/오른쪽으로 분할된 array를 각각 재귀적으로 다시 partition을 수행해줍니다.

---

아래는 Lomuto Partition방식을 이용한 QuickSort의 전체 코드입니다.

def partition(A, low, high):
    pivot_idx = low #pivot을 처음 원소로 설정
    pivot = A[pivot_idx]

    A[pivot_idx], A[high] = A[high], A[pivot_idx] #맨 처음 pivot과 마지막 원소를 swap

    i = low #low 자리에서 i 시작
    for j in range(low, high): #j가 array 처음부터 끝까지 도는 동안
        if A[j] < pivot: #A[j]가 pivot보다 작으면
            A[i], A[j] = A[j], A[i] #A[i]와 A[j] swap
            i += 1 #swap 이루어졌으면 i에 +1

    pivot_idx = i
    A[pivot_idx], A[high] = A[high], A[pivot_idx] #loop 마치면 A[i]와 pivot swap

    return pivot_idx


def quick_sort(A, low, high):
    if low < high:
        pivot_idx = partition(A, low, high) #pivot 기준 partition 진행
        quick_sort(A, low, pivot_idx - 1) #partition의 왼쪽 array에 대해 재귀
        quick_sort(A, pivot_idx + 1, high) #partition의 오른쪽 array에 대해 재귀

3. 퀵 정렬 시간복잡도/공간복잡도

시간복잡도:

Best Case:

Partition 하는 과정에서는 j가 array를 한 번 도는 수행시간을 가지므로: O(n)의 시간을 갖습니다.

이제 Quick sort에서 재귀적으로 정렬을 하는 과정은 아래와 같습니다.

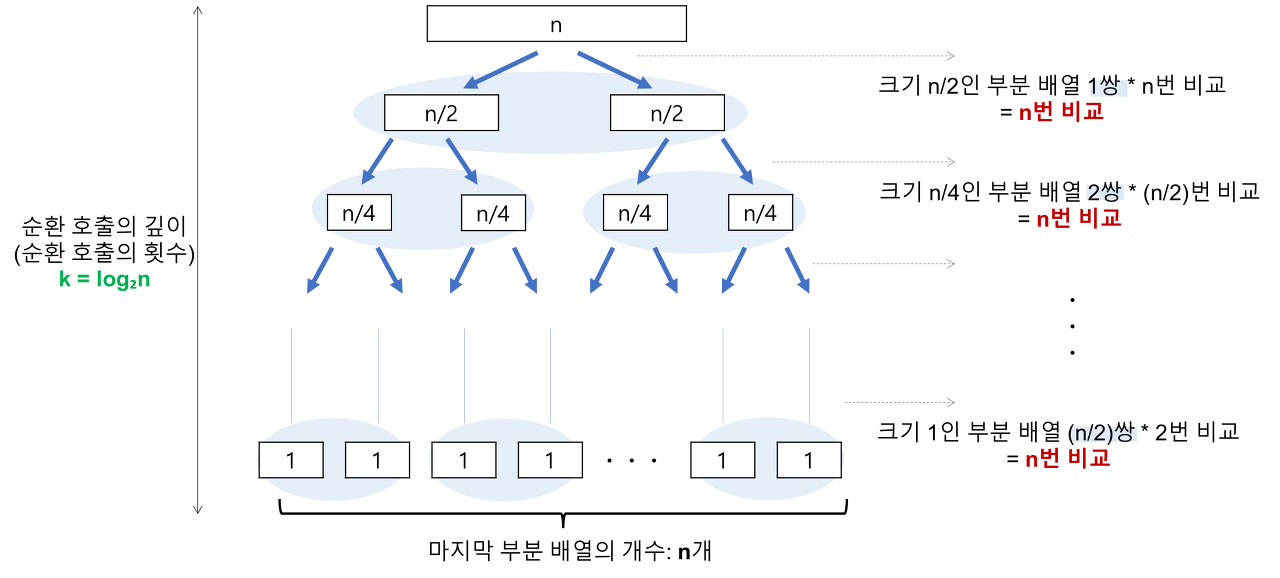
• 이진 트리의 구조를 가지고, 재귀적으로 array를 분할해나갑니다.
• 퀵 정렬은 pivot이 정확히 가운데에 위치하여 절반씩 array를 쪼개나가는 경우가 Best Case 입니다.
• 이 경우에는 절반으로 array가 나눠지므로, 전체 정렬 시간은 n/2 array 두개를 정렬하는 시간과 같을 것입니다. 따라서 2T(n/2) 의 시간을 갖습니다.
• 정리하면, 퀵 정렬에서 소요되는 총 시간은 Partition 과정 시간 + 재귀적 sort 시간 이므로: 2T(n/2) + O(n) 입니다.

이때, 이진 트리의 성질에 따라 순환 호출의 깊이는 log n 값을 갖고, leaf 노드의 개수는 n개 이므로, T(n/2) = n(log n - 1) 값을 가지며, 퀵 정렬의 시간복잡도는 2n(log n - 1) + O(n) 이 됩니다.

이를 Big O notation으로 간단히 표현하면 O(nlogn) 값을 가집니다.

Worst Case:

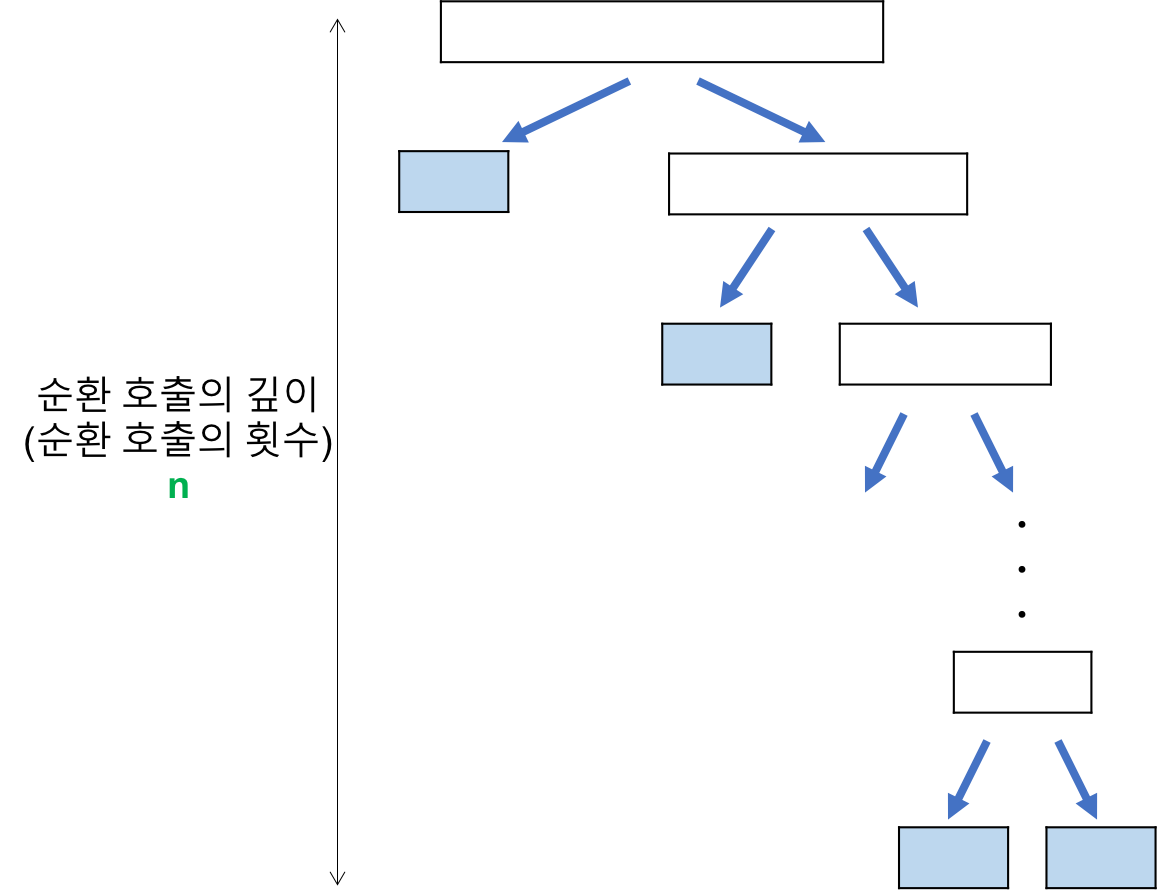
• 퀵 정렬에서의 Worst Case는 array가 오름차순 또는 내림차순으로 정렬되어 있는 경우입니다.
• 이 경우에서는 위 그림처럼 절반으로 쪼개지는 것이 아니라, T(0) + T(n-1) 로 쪼개집니다.
• 총 array의 개수만큼 순환 호출 횟수가 발생하므로, 총 깊이는 n입니다.
• 여기서도 마찬가지로 leaf노드의 개수는 n개 이므로, 재귀 과정에서는 n * n으로 O(n^2) 의 시간 복잡도를 갖습니다.

Partition은 마찬가지로 O(n)의 수행시간을 갖기 때문에,

정리하면, 퀵 정렬의 Worst Case의 경우 O(n^2) + O(n)의 시간복잡도를 갖습니다. 즉, O(n^2) 의 시간복잡도를 갖습니다.

Average Case: 퀵 정렬의 Average Case는 Best Case의 경우와 유사합니다. 따라서 O(nlogn) 의 시간복잡도를 갖습니다.

---

공간복잡도:

추가적인 Memory의 요구가 없는, In-place sort 방식입니다. 주어진 메모리 안에서만 정렬합니다.

따라서, 퀵 정렬은 O(1) 의 공간복잡도를 갖습니다.